Daily Diet For Weight Loss: Multiplication Pin Explained

In today's post we featured this pin:

http://themetapicture.com/the-japanese-way/

It took me a while to figure out what they did, but it's awesome. We've had some requests to explain how to do this and make it work, so using my super high tech Microsoft Paint program, I'll walk you through how to do this multiplication trick.

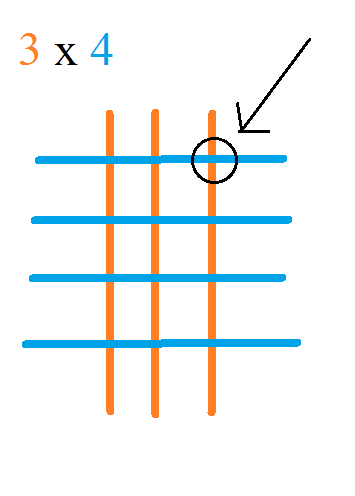
We'll start with multiplying single digits together. We'll do 3x4. I tried to "color code" each number (I'm sorry to those with color blindness, like my husband...the colors won't help a whole lot, I know).

Start with the first number, 3. Draw 3 vertical lines.

Next, go to your second number, 4. Draw 4 horizontal lines across the vertical lines you just drew.

Now, you are looking for the intersections of the lines (where they cross):

Count all the intersections, and you have your answer:

So now, what about multiplying numbers with double digits?
Let's look at the problem in the original pin, 13 x 12.

Start with the first digit of the first number. In this case that's the 1 of the 13. Draw 1 vertical line.

Now move on to the second digit in the first number. That would be the 3 of the 13. Spaced to the right of your first vertical line, draw 3 vertical lines grouped together.

Now let's move to 12. Take the first digit of the second number. That would be the 1 of the 12.
Draw 1 horizontal line at the top.

Then take the second digit of the second number. That's the 2 of the 12. Spaced below your first vertical line, draw 2 vertical lines grouped together.

Now, we need to group the intersections. We do this in diagonals from the top left corner, working down to the bottom right corner. Circling the groups helps keep everything all in place in your head. See the graphic below:

Each circle/oval counts as one group.

Now we count up the intersections for each group we just circled in the previous step.

Working clockwise around the drawing gives you your answer. Always start at the upper left corner and then follow the numbers in sequence. 1, 5, 6. 13 x 12 = 156

Let's look at another double digit problem. Start by making you vertical lines to represent your first number in the problem.

Add the horizontal lines for your second number.

Circle your groups.

Count up the intersections in each group.

Now here's where this one changes a little. The answer to 15 x 23 is not 21315. When you run into a problem that produces groups that have intersections in the double digits (like the 13 and the 15 in this problem). You have an extra step you have to take.

Start with the first double digit grouping in your drawing. In this case that's the 13. You are going to take just the first digit (the 1) and add it to the group directly to the left (the 2). See the brown underline I did in the graphic below. Write the sum of the two numbers above the drawing. I find it easy to draw lines from the numbers to their sum so I know for sure what numbers are referring to.

Still working with that 13, we are now going to take the 3 and add it to the first digit of the next number working clockwise around the drawing. So we end up with 3 + 1 (see the numbers I have underlined in purple in the graphics below).

At this point it may be easy to cross out the numbers you used to add up to your new numbers. Was that clear as mud? Here:

Now that you have just single digit numbers around your drawing, you have your answer. As before, start with the first number and work clockwise around the drawing: 3, 4, 5. 15 x 23 = 345